En la entrega anterior vimos los fundamentos de las técnicas de conversión entre diferentes profundidades de color, y dejamos de lado la conversión a 8 bits por pixel (paletizados) ya que ello requería algunos conceptos que no se habían visto en ese momento. Dichos conceptos van a ser tratados en el presente artículo, comenzando por el concepto y rutina de búsqueda en una paleta del color más cercano a uno dado.
paleta = (0,0,0), (0,0,1), (53,23,23)Si se busca el color más similar al (53,20,20), obviamente el color más parecido será el nº 2 (color (53,23,23)), que aunque no es exactamente igual al buscado, sí que es prácticamente igual de tonalidad y luminosidad en pantalla y es mucho más parecido que el resto de los colores en la paleta.
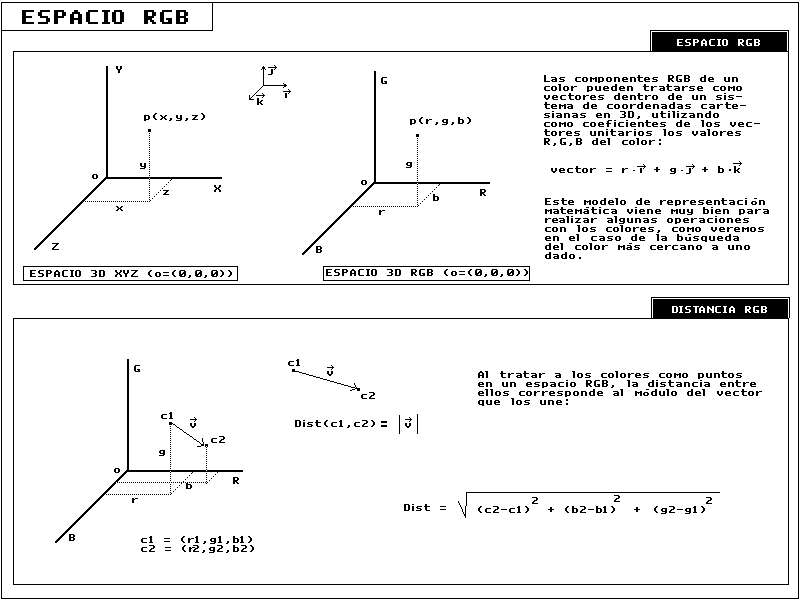
La pregunta es: ¿cómo buscar el color más parecido? Bien, concretando un poco en el lenguaje, nótese que encontrar el color más parecido a otro significa encontrar el que tenga menos diferencia con éste. Si tratamos los colores como puntos en un sistema de coordenadas 3d (espacio RGB -> RGB = XYZ), nos damos cuenta de que cuanto más parecidos son los colores, más cercanos están, y viceversa. En palabras sencillas, cuanto menor es la distancia entre los colores, más parecidos son (ver figura 1).

La distancia entre 2 puntos es, como puede verse en la figura 1, el módulo del vector que los une. De esta manera, la distancia entre 2 colores RGB es:
dr = r2 - r1; dg = g2 - g1; db = b2 - b1; dist = sqrt( dr*dr + dg*dg + db*db );Para encontrar el color más parecido a otro, se recorre la paleta desde el color 0 hasta en 255 calculando las distancia de nuestro color buscado con el de la paleta. Aquel que nos dé la menor distancia de toda la paleta será el más parecido al original (aunque no tiene porqué ser una buena aproximación).
Lo que realmente se busca con NearestColor() es una relación entre las distancias (no nos interesa la distancia exacta, tan sólo cual es la menor), por lo que podemos prescindir de la operación de raíz cuadrada sqrt() para acelerar el proceso, utilizando tan sólo los cuadrados de las componentes del vector:
dist = dr*dr + dg*dg + db*db;De esta manera, una rutina/algoritmo de búsqueda del color más cercano a otro quedaría como en el listado 1.
LISTADO 1: Nearest Color.
//-----------------------------------------------------
// Algunas macros útiles para NearestColor:
//-----------------------------------------------------
#define RED(pal,col) ((pal)[(col)*3])
#define GREEN(pal,col) ((pal)[(col)*3+1])
#define BLUE(pal,col) ((pal)[(col)*3+2])
#define byte unsigned char
//-----------------------------------------------------
// int NearestColor( r, g, b, paleta );
// Busca el color más parecido a rgb en paleta.
//
// Devuelve -1 en caso de error (improbable).
//-----------------------------------------------------
long NearestColor( byte r, byte g, byte b, byte *paleta )
{
long result = -1; // color mínimo hasta ahora
long minimo = 200000; // distancia mínima "" ""
long rd, gd, bd; // componentes vector c2-c1
long dist, i; // distancia e índice bucle
// repetimos para los 256 colores:
for( i=0 ; i<256 ; i++ )
{
// componentes del vector: r2-r1, etc.
rd = r-RED(paleta, i);
gd = r-GREEN(paleta, i);
bd = r-BLUE(paleta, i);
// calculamos la distancia:
dist = rd*rd + gd*gd + bd*bd;
// comprobamos si es la menor hasta ahora:
if( dist <minimo )
{
// es la menor: lo anotamos y seguimos
minimo = dist ;
result = i;
}
}
return( result );
}
Mediante la rutina de Nearest Color podemos crear tablas lookup con gamas de azules, rojos o verdes precalculados para realizar efectos de luces en modos de 8bpp. Por ejemplo, si disponemos de una imagen y queremos simular una luz (flare) moviéndose sobre ella (o dejando estelas de un color concreto), podemos hacer una tabla de 63 elementos, por ejemplo, que indiquen el color más parecido a cada posible gama de rojo, es decir, en tabla[0] el más parecido a (0,0,0), en tabla[10] el más parecido al (10,0,0), etc. y utilizar esta tabla para mover una luz sobre la pantalla.
Permite trazar en pantalla bitmaps con diferentes paletas. Por ejemplo, Windows mapea constantemente las paletas de las diferentes ventanas para que todas ellas tengan una paleta aceptable en 8bpp.
Convertir un bitmap de un número determinado de colores (por ejemplo 256) a otro (241, 128, etc.) con el fin de disponer de entradas libres en la paleta para realizar otro efecto con la misma.
Utilizarla para los filtros de imágenes bajo 8bpp, como veremos en un próximo apartado.
El problema tal y como se ha presentado (convertir 16 millones de colores en 256) resulta muy difícil de abordar, pero en la práctica son pocas las imágenes que utilicen tal número de colores distintos. Una imagen 320x200 TrueColor puede contar (por ejemplo) con 10.000 colores distintos aunque tenga 64.000 píxels, ya que muchos colores pueden estar repetidos (por ejemplo, la foto de un cielo contendrá muchos azules repetidos). Además, muchos de esos 10.000 colores pueden ser colores muy cercanos entre ellos (por ejemplo, 2 píxels (120,0,0) y (122,0,0) son difícilmente distinguibles y los veremos como 2 colores iguales).
Aun así, la rutina de conversión que hemos de realizar habrá de convertir una imagen de un número elevado de colores en tan sólo 256, lo cual se antoja, a primera vista, complicado.
Comentamos pues el más sencillo método de conversión: el método del histograma de frecuencias. Este método se basa en los 2 fenómenos comentados en el ejemplo de conversión anterior:
Prácticamente siempre hay colores (r,g,b) que se repiten en una imagen (muchos píxels del mismo color, como por ejemplo un fondo negro, con muchos píxels (0,0,0)).
La mayoría de las imágenes contienen muchos degradados, es decir, algunos colores son muy parecidos a otros salvo en un par de unidades en alguna de las componentes, y prácticamente puede decirse que a la vista son iguales.
Basándonos en los puntos anteriores, puede crearse una rutina que coja los 256 colores más utilizados de la imagen y los use como la paleta de la imagen. Es decir, calcularemos cuales son los 256 colores que más se utilizan y almacenaremos los valores RGB de esos componentes en un array del tipo:
char paleta[256][3];A continuación se tiene que convertir cada pixel de la imagen a un color de esa paleta. Los colores que estén incluidos dentro de la paleta (porque eran de los más utilizados) tendrán una conversión perfecta y sencilla: en la imagen final almacenaremos el índice a dicho color en nuestro array, por ejemplo, si el (23,54,23) está situado en la posición 23 del array de paleta, escribiremos en el destino como valor del pixel el nº 23 (no olvidemos que en 8bpp un color es una referencia a un array de componentes llamado paleta).
Si el pixel de la imagen original que estamos considerando no está en la paleta, obviamente no podremos escribirlo en la imagen destino: lo que se hará será buscar en la paleta el color más parecido al original (mapear el color: de entre los 256 que tenemos, buscar cuál es más parecido, obtener la mejor aproximación posible), y almacenarlo en el destino.
Repitiendo esto para todos los pixels de la imagen obtendremos una aproximación en 8bpp (bastante buena la mayoría de las veces) a la imagen original.
a). Seleccionar los 256 colores más usados: La manera más sencilla de hacer esto es utilizar una array cúbico de 256x256x256 elementos:
frecuencia[256][256][256] ;Este array se usará como un indicador de la frecuencia de aparición de cada color: cada elemento del array indica el número de pixels de la imagen para cada color RGB, es decir, si en una imagen hay 10.000 colores (0,0,0), entonces frecuencia[0][0][0] = 1000.
Para crear la tabla completa simplemente tendremos que recorrer la imagen original y anotar en el array cada color encontrado:
for( ... alto_img ... )
for( ... ancho_img ... )
r,g,b = GetPixel();
frecuencia[r][g][b]++;
Tras hacer esto el array contendrá la cantidad de píxels que hay de cada
color, y como es lógico, si seleccionamos los más frecuentes (los 256
elementos del array de mayor valor), la imagen convertida será más fiel a la
original y tendremos que convertir menos colores (los restantes) a la paleta
destino.b). Buscar el color más cercano a uno dado: El proceso de búsqueda del color más parecido a otro en una paleta dada (mapear el bitmap) se ha comentado ya al principio del artículo, de modo que puede utilizarse la técnica descrita en dicho apartado para el mapeado de los colores.
a). Usar una hash table (tabla de transformación) para encontrar el color más parecido a un color ya encontrado anteriormente (se puede implementar de diferentes formas).
b). Ordenar la paleta óptima generada por un elemento (rojo, por ejemplo), mediante esto, al buscar un color primero encontramos el color más parecido al nuestro en rojo. Para ese color, se recorre el array hasta el final de la paleta usando la fórmula de búsqueda del color más cercano. Dentro de esta búsqueda, si r*r (o sqrt(r*r)) es mayor que la menor de las distancias entonces podemos abortar el loop, ya que si r*r es mayor que la distancia mínima, entonces seguro que r*r+g*g+b*b es mayor que esta distancia mínima. Como nuestra tabla estaba ordenada de menor a mayor, sabemos que el resto de los elementos de la tabla son de distancia mayor que el que estamos considerando, con lo que hemos encontrado el más cercano (cesamos la búsqueda hasta el final).
Es muy recomendable indagar y buscar en Internet o libros especializados otros tipos de rutinas de cuantización de color más eficientes. Algunas referencias recomendadas son:
- http://ourworld.compuserve.com/homepages/cmetric.htm
- XV, visualizador de gráficos bajo Linux,
(en cualquier distribución de Linux; con 3 tipos distintos
de cuantización de color).
- http://www.inforamp.net/(poynton/Poynton-color.html
Lo recomendado a la hora de soportar distintas resoluciones para una
aplicación windowed es disponer en el disco duro de un set de gráficos en
truecolor y otro en paletized (obtenido por ejemplo con programas como Alchemy
o PhotoShop), utilizando estos últimos si el display está en 8bpp y los
primeros para convertirlos fácilmente al resto de formatos normalmente
utilizados (15/16/24/32 bpp).
Existen infinidad de filtros que pueden se aplicados a una imagen con el fin de poder obtener un gráfico más luminoso, oscuro, borroso, resaltado, definido, etc. que el original. Por tanto esto no es más que un "filtro", como su palabra indica, por el que se pasa la imagen obteniendo la misma pero de diferente textura.
Como ejemplo, si vemos una imagen tras pasar por un filtro, la imagen filtrada se diferencia de la original en que se ha logrado detallar y resaltar sus pixels en los lugares donde más lo necesita (como en el contorno y en los bordes que delimitan dos superficies o planos diferentes dentro de la misma imagen). Filtrar una imagen es aplicarle una transformación para obtener otra imagen parecida a la original pero distinta en esencia.
Ahora que conocemos más o menos lo que es un filtro y que efectos puede producir sobre una imagen, tenemos que saber como aplicar uno de estos a una imagen nuestra para utilizarlo en el desarrollo de juegos o utilidades.
Height-based (basado en la altura) Color-based (basado en el color)El filtro basado en la altura (Height-based) sólo trabaja con colores indexados. Esto quiere decir que debemos trabajar con imágenes de 8bpp donde tenemos colores de 0-255 como índices a los RGB guardados en un array de paleta[256][3]. Con esto tenemos una paleta con la cual no damos posibilidad de más colores de los que contiene esta y con los que debemos trabajar únicamente. Debido a esto si queremos filtrar una imagen de 8bpp no podemos coger los pixels de pantalla y hacer con ellos la media ya que podría darnos como resultado un valor de la paleta que contiene un color muy diferente al que debía darnos.
Debemos de trabajar con las componentes RGB del color, que son las que nos van a definir la tonalidad del color. Es ahora cuando llega el problema para los modos de 256 colores que al hacer la media de todos los R, los G y los B nos puede dar un valor que no existe en la paleta, con lo cual deberemos de buscar el color más parecido a este.
Sin embargo, los filtros basados en el color se refieren a filtros que trabajan sobre imágenes de más de 8bpp, y que por lo tanto no estamos obligados a trabajar sobre unos colores predeterminados (paleta).
0 0 0 0 0 0 0 1 0 0 0 1 * 1 0 0 0 0 0 0 0 0 0 0 0Lo que se hace con esta matriz es para cada pixel que esté a 1 (tomando * como el pixel actual y recorriendo toda la pantalla), coger ese color, sumarlo al resto tomado hasta ahora y finalmente realizar la media del total. Es decir, hemos multiplicado cada pixel por el valor que le corresponde en la matriz (0*color=0, 1*color=color) y los hemos sumado todos juntos. Si cambiamos los números de la matriz de arriba por otros números, estaremos aplicando un filtro distinto.
Una cosa que hay que tener en cuenta sobre el efecto fuego es que el suavizado que forma el filtro para el efecto fuego se produce ya que la paleta de 256 colores está preparada para eso, teniendo un gradiente de colores para que se pueda realizar correctamente. Esto no ocurre entonces en una imagen normal pudiendo tener una paleta de colores muy variada, y donde al hacer la media de 2 índices a paleta nos de como resultado otro índice que no se parece nada al color buscado, la solución es trabajar con componentes, no índices. Pero sigamos con el ejemplo del fuego:
Esta matriz es guardada en un array como información al filtro que debemos aplicar a la imagen. El valor del array [3][3] corresponde al pixel central, y lo deberemos de relacionar con el pixel escogido de la imagen para aplicar sobre este la media de los valores que lo rodean atendiendo siempre al 1 de la matriz del filtro y despreciando los 0 (sencillamente multiplicando). Por tanto, este filtro se aplica recorriendo cada uno de los pixels del gráfico y haciendo la media de este con el de arriba, abajo-derecha y abajo-izquierda (como indica su matriz de filtro). La media para cada uno de los pixels sería la siguiente :
media = imagen[x][y]+ imagen[x][y-1]+ imagen[x-1][y]+ imagen[x+1][y] media = media / 4El valor obtenido de esta media se deberá de escribir sobre el mismo pixel leído en el momento de aplicarle la matriz de filtro. De esta manera suavizamos la imagen, ya que sabemos que entre un color de la paleta y otro están los colores intermedios, con lo que haciendo la media de los índices obtenemos una media de color. Veamos ahora el código que hace todo esto sobre una pantalla de una resolución cualquiera.
for (y=top ;y<=bottom ;y++)
for (x=left ;x<=right ;x++)
{
media=imagen[x][y]+imagen[x][y-1]+imagen[x-1][y]+imagen[x+1][y] ;
media = media / 4 ;
imagen[x][y] = media ;
}
Por supuesto, la paleta estaba preparada para que al hacer la media salgan
los colores suavizados entorno a cada uno de la pantalla. El truco de la
facilidad del efecto fuego está obviamente en la preparación de la paleta. El
problema llega cuando tenemos una imagen con colores variados en la paleta
(como se comentaba antes). Supongamos una matriz de 5x5 para aplicar un filtro
a una imagen de 8bpp:
Tipo de filtro : Soften (medio) 0 0 0 0 0 0 1 3 1 0 0 3 9 3 0 0 1 3 1 0 0 0 0 0 0 dividido entre 25En este caso tomamos como punto central la posición del valor de '9', coordenada [2][2], donde haremos la media a partir de este punto. Es decir: multiplicamos el pixel actual por 9, el de su izquierda por 3, etc. sumándolos todos y dividiendo entre 25. Al tomar un valor de una coordenada de la pantalla, hacemos para este el cálculo necesario con el valor que le corresponde de la matriz, que es el '9'. Dicho cálculo lo guardamos en una variable para no perderlo. El cálculo es el siguiente :
var_r = R * 9 // R,G,B de la paleta (color leído) var_g = G * 9 Var_b = B * 9Para los pixel de la pantalla que le rodean y que corresponden con la matriz a un número diferente de 0, también realizamos los mismos cálculos sumando a cada variable los nuevos valores y dividiendo una vez acabado, entre el valor de división. Es decir, como ejemplo para el pixel de arriba :
var_r = var_r + R * 3 var_g = var_g + G * 3 var_b = var_b + B * 3Y para los restantes pixels que rodean al central hacemos lo mismo (con el valor que les corresponda en la matriz). Y dividimos:
var_r = var_r / 25 var_g = var_g / 25 var_b = var_b / 25Lo que hemos hecho, en resumen, es recorrer toda la pantalla desde (0,0) hasta (MaxX,MaxY), y a cada pixel le aplicamos la matriz de 5x5. Esto significa tomar como pixel actual el centro de la matriz, es decir, "colocar" la matriz sobre la imagen de manera que el pixel actual coincida con el elemento (3,3) de la misma, y multiplicar el color de ese punto y de los puntos vecinos por el valor de la matriz para ese punto. A continuación sumamos todos esos valores y realizamos una división a modo de media. Como no podemos trabajar con colores, sino con RGB's, hacemos esto para las componentes. Ahora es el momento de trazar en pantalla el color obtenido.
En el caso de 8bpp debemos buscar en la paleta el color más parecido al resultado (ya que sólo disponemos de 256), como se ha explicado anteriormente, y dibujarlo en la coordenada correspondiente. Para modos gráficos de más de 8bpp no será necesario buscar ningún color cercano a los de la paleta ya que carecen de ésta. Aquí tenemos un pseudocódigo para imágenes de 256 colores (8bpp):
for (y=top ;y<=bottom ;y++)
for (x=left ;x<=right ;x++)
{
gridCounter = 0 ;
total_R = total_G = total_B = 0 ;
for (y2=-2 ;y2<=2 ;y2++)
for (x2=-2 ;x2>=2 ;x2++)
{
total_R += paleta[image[x+x2][y+y2]*3] * filtro[gridCounter] ;
total_G += paleta[image[x+x2][y+y2]*3+1] * filtro[gridCounter] ;
total_B += paleta[image[x+x2][y+y2]*3+2] * filtro[gridCounter] ;
gridCounter++ ;
}
total_R /= DivisorFactor ;
total_G /= DivisorFactor ;
total_B /= DivisorFactor ;
pantalla[x][y] = NearestColor (total_R,total_G,total_B,paleta) ;
}
Y para imágenes de más de 8bpp tendríamos el siguiente pseudocódigo:
for (y=top ;y<=bottom ;y++)
for (x=left ;x<=right ;x++)
{
gridCounter = 0 ;
total = 0 ;
for (y2=-2 ;y2<=2 ;y2++)
for (x2=-2 ;x2>=2 ;x2++)
{
total += image[x+x2][y+y2] * filtro[gridCounter] ;
gridCounter++ ;
}
total /= DivisorFactor ;
pantalla[x][y] = total ;
}
comp = comp << 4; comp = comp * (255/63); comp = (comp<<2) + (comp>>4);
Aprovechamos de paso este pequeño párrafo para agradecer a los lectores su apoyo, los juegos de ejemplo que nos han enviado (hechos por ellos mismos siguiendo el curso) y los mensajes de agradecimiento. Ahora es el turno del lector: recuerde que "a programar se aprende programando".
Pulse aquí para bajarse los ejemplos y listados del artículo (6 Kb).
Figura 1: "Espacio RGB y distancias entre colores."
Santiago Romero